1.
図のように 1辺６cm の立方体がある。
(1) ４点 A, C, F, H を頂点とする立体の名称を答えよ。
(2) (1)の立体の体積を求めよ。
(1) 立体ACFHは4つの面で囲まれた多面体である。
三角錐でも良いが、すべての面が合同な正三角形なので正四面体が最も適切である。
(2)
正四面体ACFHの体積を直接出すことは無理なので、
立方体から、いらない部分を引き算して求める。
いらない部分は全て同じ形の三角錐である。
頂点Bを含む三角錐、頂点Dを含む三角錐、頂点Eを含む三角錐、頂点Gを含む三角錐の４つある。
Eを含む三角錐で体積を出してみる。
EH=EF=6なので△EFHの面積は6×6÷2=18
△EFHを底面とするとAE=6が高さとなるので
体積は 18×6÷3=36
立方体から同じ形の三角錐4つを引くので
216-4×36=72
2.
図は底面が∠CAB=∠FDE＝90°の直角三角形の
三角柱である。この立体を面 PQR で切断する。
AB=6 ㎝、AC=4 ㎝、AD=12 ㎝、BQ=6 ㎝、
AP=9 ㎝、CR=8 ㎝のとき、切断してできる小さ
いほう(下のほう)の立体の体積を求めよ。
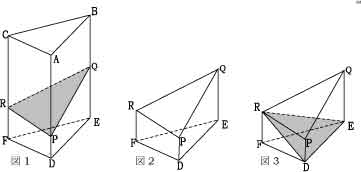求める立体だけを取り出したのが図2である。
さらにこれを図3のように面RDE で切断する。
すると三角錐RFDEと四角錐RPDEQに分かれる。
三角錐のほうは底面が△FDE,高さがRFである。
△FDE の面積12cm2, RF=4cm より体積16cm3
また、四角錐のほうは底面が台形PDEQ である。
高さはRから面ADEBにおろした垂線の長さで、
これは辺FDと同じ長さになる。
台形ADEB の面積(3+6)×6÷2=27 FD=4cm
より体積36cm3
よって求める立体の体積は16+36=52
3.
右の図のように 1 辺 6cm の立方体がある。
AJ=AK=2cm である。4点J,K,H,Fを通る平面で2つの
立体に分ける。頂点Aを含むほう(小さいほう)の
立体の体積を求めよ。
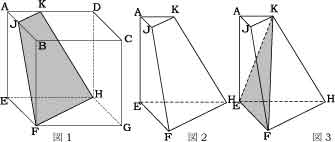求める立体を取り出したのが図2 である。
さらに面KEF で切断したものが図3 である。
すると四角錐KAEFJ と三角錐KEFH に分かれる。
四角錐は台形AEFJ を底面として高さがAK なので
(2+6)×6÷2×2÷3=16 体積16cm3
三角錐は△EFH が底面で
Kから面EFGHにおろした垂線の長さが高さである。
よって体積は6×6÷2×6÷3=36
よって36+16=52 となる
4.
右の図は底面が一辺6㎝の正方形の四角錐である。
また、高さは10cmである。AF=3㎝、BE=2㎝、BP:PO=3:2
のとき、三角錐PFEDの体積を求めよ。
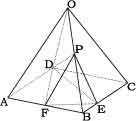四角錐OABCD の高さが10cm でBP:PO=3:2 より
三角錐PDFE の高さは6cmとなる。
底面の△DFE は正方形ABCD から△ADF,△BEF、△DEC を
引けば出るので
36-9-3-12=12
よって体積 12×6÷3=24
5.
図のように AB=6cm, BC=10cm, AD=12cm、
∠ABC=∠DEF=90°の三角柱 ABC-DEF がある。
M は AC の中点、N は BC の中点で、MN=3cm である。
このとき A, B, N, M, D, E を頂点とする立体の体積を求めよ。
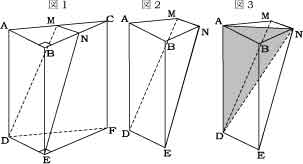求める部分を取り出したものが図2,
さらに面ANDで切断し,三角錐DANMと
四角錐NADEBに分ける（図3）
三角錐のほうは底面が△ANMで高さがAD
よって体積が3×5÷2×12÷3=30
四角錐は底面が長方形ADEB、高さがBN
よって体積が6×12×5÷3=120
求める体積は120+30=150
