1. 図の台形はAB=18cm, BC=8cm,
CD=12cm, ∠ABC=∠BCD=90° である。
点Pが頂点Aを出発してA→B→C→Dと毎秒2cmで進む。
出発してからx秒後の△APDの面積をycm2とする。
次の問に答えよ。
(1)点Pが辺AB上にいるときについて
①xの変域を求めよ。
②yをxの式で表せ。
(2)点Pが辺BC上にいるときについて
①xの変域を求めよ。
②yをxの式で表せ。
(3)点Pが辺CD上にいるときについて
①xの変域を求めよ。 ②yをxの式で表せ。
点Pは毎秒2cmずつ進むので、出発からx秒後までに移動した距離は2x(cm)となる。
(1)
① AP=2xなので、PがBに着くのは2x=18 つまり9秒後
よってxの変域は0≦x≦9
② △DAPは底辺2x, 高さ8なので
面積y = 2x×8÷2= 8x
式は y=8x
(2)
① (1)より 点PがBに到着するのは出発から9秒後
AからBを通ってCまでは18+8=26cmなので、
毎秒2cmでCに到達するのは出発から13秒後
よって変域は 9≦x≦13
② 直接△APDの面積は出せないので、
台形ABCDから、△PABと△PCDの面積を引く。
台形ABCDの面積 (12+18)×8÷2=120
△PABの面積
図で赤い線で示した部分がPが通った道のり2x
よってPB=2x-18 これが高さ
AB=18 が底辺である。
面積 18×(2x-18)÷2=18x-162
△PCDの面積
高さ PC=26-2x
底辺 CD=12
面積 12×(26-2x)÷2=156-12x
△APD = 台形ABCD - △PAB -△PCDなので
y =120 -(18x-162) -(156-12x)
よって y=-6x+126
(3)
①
(2)より 点PがCに到着するのは出発から13秒後
AからB,Cを通ってDまでは18+8+12=38cmなので、
毎秒2cmでDに到達するのは出発から19秒後
よって変域は 13≦x≦19
② 図の赤い線がPが通った道のり2x
よって底辺 DP=38-2x
高さCB=8
面積 (38-2x)×8÷2=152-8x
式 y=-8x+152
【別解】
1次関数の式として考える。
(1)辺AB上のとき
Pが点Aにいるのは0秒のときで、△APDの面積は0、
つまりx=0, y=0 これをグラフの座標で表すと(0,0)
毎秒2cmで、Pが点Bに来るのはスタートから9秒後、
このとき、△APDは△ABDと同じなので 面積は18×8÷2=72つまり座標は(9,72)
点(0,0)と(9,72)の2点から式を求めるとy=8x
(2)辺BC上のとき
Pが点Bに来たときは(9,72)
そして点Cに来たとき、これはスタートから13秒後
△APDは△ACDと同じなので、面積は12×8÷2=48
つまり座標は(13,48)
(9,72)と(13,48)を通る直線はy=-6x+126
(3)辺CD上にいるとき
Pが点Cにきたとき(13,48)
そして点Dにきたとき、スタートから19秒後、面積0 よって(19,0)
(13,48)と(19,0)を通る直線はy=-8x+152
2.
図は長方形ABCDである。Pは点Aを出発して毎秒1㎝で
A→B→C→Dと進む。
Pが出発してからx秒後の△APDの面積をycm2とする。
xとyの関係を表したのが下のグラフである。
(1) 辺AB, BCの長さを求めなさい。
(2) グラフのmの値を求めなさい。
(3) △APDの面積yを表す式を書きなさい。(xの変域も)
動点PがA→B→C→Dとすすむ。 グラフではAのとき(0,0), Bのとき(5,50), Cのとき(m,50)となる。
(1) 毎秒1cmで、5秒後にBに来るのでAB=5cm
△ABDの面積が50cm2、AB=5cmなので 50=AD×5÷2
AD=20cm, BC=ADなので BC=20cm
(2) AB=5, BC=20なので点Cに到達するのは出発から25秒後 よってm=25
(3)
グラフを見れば3つの直線でできていることがわかる。
それぞれ2点から直線の式を求めることができる。
5≦x≦25 では(5, 50)を通りx軸に平行なのでy=50
25≦x≦30では(25,50)と(30,0)から式を求めると y=-10x+300
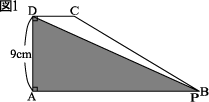
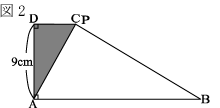
3.
図1の点Pは毎秒1cmでA→B→C→Dと進む。
Pが出発してからx秒後の△APDの面積をycm2
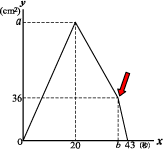
としてグラフにしたものが図2である。
(1)辺AB、辺BC、辺CDの長さを求めよ。
(2)グラフのa、bを求めよ。
(3)Pが辺CB上にいるときについてyをxの式で表せ。
(4)y=72となるのは何秒後か。
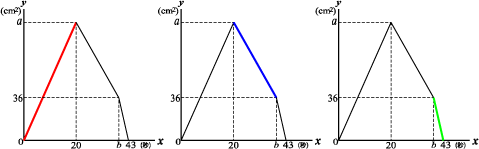
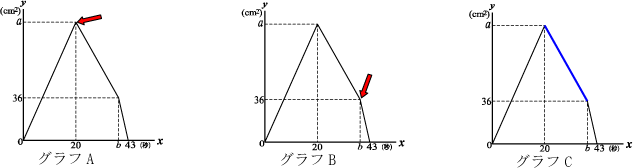
まず点Pの位置とグラフの関係
を確かめる。
点Pが辺AB上を動いていくとき
のグラフは図の赤い直線となる。
点Pが辺BCを動くときのグラフ
は青、点Pが辺CD上を動くとき
は緑である。
(1),(2)
図1のように点Pがちょうど頂点Bに来たとき、
座標は右下のグラフの矢印で示した点となる。
この点のx座標は20、つまり出発から20秒後である。
出発した点Aから点Bまで20秒かかり、毎秒1cm
なので、AB=20cmとなる。
さらに底辺20cm、高さ9cmの三角形の面積は90cm2
なのでy座標が90となる。つまりa=90である。
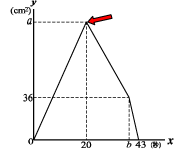
次に図2のように点Pが頂点Cに来たとき、
座標は右下のグラフの矢印の点である。
図2で高さ9cm,底辺CD、グラフから
面積は36cm2なのでCD=8cmになる。
すると、Pが毎秒1cmの速さで辺DC上をCからDまで
動く時間は8秒間となる。
グラフからPがDに到着するのが43とわかっているので
43-8=35 となり b=35である。
BからCまでは35-20=15秒かかり、
毎秒1cmなのでBC=15cm
(3)
(2)で出した、a=90,b=35の値を用いる。
グラフAの矢印が指す座標が(20, 90)、
グラフBの矢印が指す座標がが(35, 36)、
この2点からグラフCの青い直線の式が出る。
y=-185x+162
(4)
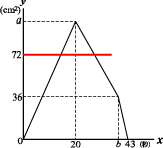
次に面積が72cm2になる場合について
グラフにy=72の線を書き入れたときの
交点のx座標が求める時間となる。
よって72=92x これを解くとx=16
72=-185x+162 これを解くとx=25