平方根応用(図形)1,2,3　解説

1. 図の△ABCはAB=AC,∠BAC=90°の
直角二等辺三角形である。
頂点Aから辺BCに垂線をおろしその交点をPとする。
AP=2cm, BC=4cmのとき次の問いに答えよ。
(1) △ABCの面積を求めよ。
(2)辺ABの長さを求めよ。

(1) 底辺をBCとすると、高さがAPなので
面積は 4×2÷2=4
(2) △ABCは直角二等辺三角形なので
辺ABを底辺とすると高さがACになる。
AB=AC=xとすると 面積を求める式は x×x÷2
(1)より面積は4なので　x²2=4
x²=8
xは8の平方根なので x=±22
長さは必ず正になるのでx>0　
よって　x=22

2. 図の四角形ABCDは正方形である。（一目盛りを1cmとする）
(1) この正方形ABCDの面積を求めよ。
(2) この正方形ABCDの一辺の長さを求めよ。

(1) 図の赤い三角形の面積は3×2÷2=3
同じものが全部で4つある。　≫
中央の正方形の面積は1なので
正方形ABCDの面積は 3×4+1=13
(2) 正方形ABCDの面積が13なのでその辺をxとすると
x² =13
xは13の平方根なので　x=±13
長さは必ず正なので x>0
よってx=13

3. 表面積が30cm²の立方体がある。
(1) この立方体の1辺の長さを求めよ。
(2) この立体の体積を求めよ。

(1) 立方体は６面すべてが合同な正方形である。
表面積が30なら、１つの正方形の面積は 30÷6=5となる。
面積5の正方形の１辺をxとすると　x²=5
xは5の平方根なので x=±5
長さは必ず正の数なので　x=5
(2) 一辺の長さが5の立方体の体積は
5×5×5 = 55

4. 図の①～③のそれぞれの正方形の1辺の長さを求めよ。（一目盛りを1cmとする）

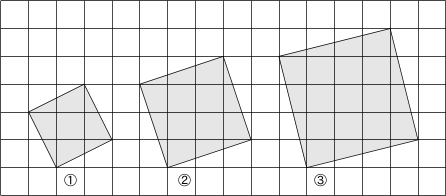
① 真ん中の正方形(青)は1辺1cmなので面積= 1×1 =1cm²
　　　赤い直角三角形は高さ2cm, 底辺1cmなので　面積 = 1×2÷2 =1cm²
三角形は4つあるので 1×4 =4
よって①の正方形の面積=1+4 = 5cm²
1辺の長さを2乗したものが正方形の面積なので
面積5cm²の正方形の1辺は 5cm

② 真ん中の正方形(青)は1辺1cmなので面積= 2×2 =4cm²
　　　赤い直角三角形は高さ3cm, 底辺1cmなので　面積 = 1×3÷2 =32cm²
三角形は4つあるので 32×4 =6
よって②の正方形の面積=4+6 = 10cm²
1辺の長さを2乗したものが正方形の面積なので
面積10cm²の正方形の1辺は 10cm

③ 真ん中の正方形(青)は1辺3cmなので面積= 3×3 =9cm²
　　　赤い直角三角形は高さ4cm, 底辺1cmなので　面積 = 1×4÷2 =2cm²
三角形は4つあるので 2×4 =8
よって③の正方形の面積=9+8 = 17cm²
1辺の長さを2乗したものが正方形の面積なので
面積17cm²の正方形の1辺は 17cm

学習 コンテンツ

練習問題 各単元の要点 pcスマホ問題 数学の例題

学習アプリ

中1 計算問題アプリ　方程式
中1数学の方程式の計算問題を徹底的に練習