1辺6cmの正八角形の面積を求めよ。
図のように補助線をひき、各点に記号をつける。
正八角形の一つの内角は 135°なので
∠HAK=90°、∠BAK=45°また、∠AKB=90°である。
すると△AKBが直角二等辺三角形になるので
AB=6cm, AK=BK=32cmとなる。
△CLD, △FME, △HNG も同様になる。
それら直角二等辺三角形の面積は 32×32÷2=9
これが4つあるので 9×4=36
四角形 AKNH は AH=6cm, AK=32cmの長方形。
BKCL,LDEM,MFGN、も同様である。
面積は 6×32=182
これが4つあるので 4×182=722
四角形 KLMN は1辺 6cm の正方形なので面積は 6×6=36
すべての和をもとめると36+722+36=72+722
AB⊥CE, AC⊥BD, 点FはBDとCEの交点である。
∠ABC=45°、 AE:EB=1:2, AC=5cmのとき
(1) ECの長さを求めよ。
(2) EFの長さを求めよ。
(1)
△EBC で∠BEC=90°、∠EBC=45°なので
∠ECB も 45°となり△EBC は EB=EC の
直角二等辺三角形とわかる。
よって AE:EB=1:2 から AE:EC=1:2 なので
AE=x とすると EC=2x, AC=5 となる。
△AECで三平方の定理を使うと
x2+(2x)2=52
5x2=25
x2=5
x=±5 x>0 なので x=5
EC=2x なので EC= 25
(2)
△ABD と△ACE において
∠ADB=∠AEC=90°、∠BAD=∠CAE(共通)
2組の角がそれぞれ等しいので△ABD∽△ACE
よって∠ABD=∠ACE・・・①
△FBE と△ACE において
∠ABD=∠ACE(①より)
∠FEB=∠AEC=90°、EB=EC(直角二等辺三角形)
よって1辺とその両端の角がそれぞれ等しいので△FBE≡△ACE
よって FE=AE
(1)で出したように AE=5 なので EF=5
図のようにAD=12㎝、AB=24㎝の長方形ABCDの
頂点Bを頂点Dに重ねるように折り返す。
このときDEの長さを求めなさい。
DEはBEを折り返した部分なので、DE=BE=x
するとAE = AB − BE =24 − x
直角三角形AEDで三平方の定理を使うと
DE2 = AD2 + AE2
x2 = 122 + (24−x)2
x2 = 144 + 576 − 48x + x2
48x = 720
x = 15
図のの△ABCの面積を求めよ。
AからBCにおろした垂線の足をDとして、
BDの長さをx, ADの長さをyとする。
2つの直角三角形△ABDと△ACDができる。
△ABDで三平方の定理を使うと
152=x2+y2・・・①
△ACDで三平方の定理を使うと
132=(14-x)2+y2・・・②
①-② =
152-132=x2-(14-x)2
56 = 28x-196
-28x=-256
x=9・・・③
③を①に代入する
152=92+y2
y2=144
y=±12
y>0よりy=12
ADは高さなので 14×12÷2=84
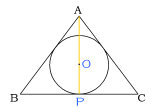
図のような二等辺三角形の三辺に接する円がある。
AB=AC=10cm,BC=12cmのときこの円の半径を求めよ。
図1のようにAからBCに垂線を引いて交点をPとする。
△ABCは二等辺三角形なのでこの線は円の中心Oを通り、
点PはBCの中点になる。
するとAC=10cm, PC=6cmとなり△APCで三平方の定理を使うと
AP2 + 62 = 102
これを解くと AP = 8
図1
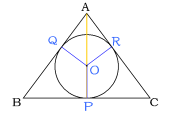
次に各接点から中心に線を引く。
円外の点から引いた接線の長さは等しいのでCP=CR=6
AC - CR = AR なので 10-6=4 でAR = 4
OP, OQ, ORは円の半径なのでこれをxとする。
OP = OQ = OR = x , AP = 8なので AO = 8 - x
ここで直角三角形AORで三平方の定理を使う。
AO2 = OR2 + AR2
(8 - x2)= x2 + 42
これを解くとx=3
図2
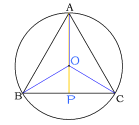
図のように円に内接する△ABCがあり、
AB=AC=17cm,BC=16cmである。この円の半径を求めよ。
図1のようにAからBCに垂線を引く。
APは中心Oを通りPはBCの中点なのでPC=8。
AC=17で、△APCで三平方の定理を使うと
AP2+82=172
AP2 = 225
AP=±15
AP>0よりAP=15
図1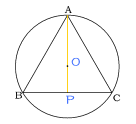
つぎにA,B,Cから点Oに線を引く。
これは半径なのでAO=BO=CO=x
OP=15-x、CO=x、CP = 8 となる。
直角三角形OPCで三平方の定理を使うと
x2 = (15-x)2 + 82
これを解くと x= 28930
図2