1
図は底面が１辺6cmの正三角形で、高さが6cmの三角柱である。
頂点A, E, Cを通る平面でこの立体をきるとき
頂点Bから面AECに下ろした垂線の長さを求めなさい。
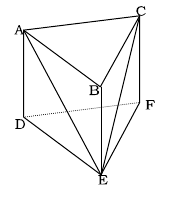
頂点Bから面ABCに下ろした垂線の長さは、三角錐BAECで△AECを底面にしたときの高さのこと。
そのため、三角錐BAECの体積と△AECの面積を出せば
三角錐の体積 = 底面積×高さ÷3 の式に代入して高さを出すことができる。
そこでまず三角錐BAECの体積を出す。
底面を△ABCとすると高さはBEである。
△ABCは一辺6cmの正三角形、またBE=6cmである。
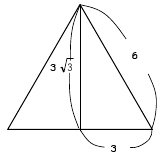
△ABC・・・図１
△ABCの面積は
底辺6cm, 高さ33cmなので
6×33÷2=93
錐の体積=底面積×高さ÷3なので
93×6÷3=183
三角錐BAECの体積は183cm3となる。
図1
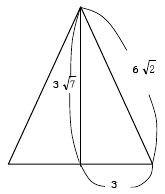
次に△AECの面積を求める。
AE, ECともに1辺6cmの正方形の対角線なので
AE=EC=62の二等辺三角形となる。・・・図2
この二等辺三角形AECの高さは
三平方の定理より
(62)2 = 32+x2
x = 37
よってこの二等辺三角形AECの面積は
97cm2となる。
図２
三角錐の体積 = 底面積 × 高さ ÷ 3 の式に
三角錐の体積・・・183、
△AECの面積・・・97、
高さ・・・h
として代入すると
183 = 97 × h ÷ 3
h = 6721
2
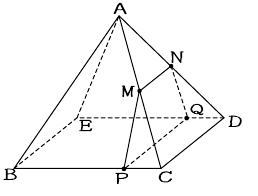
図の正四角錐は底面が1辺12cmの正方形で
それ以外の各辺はすべて10cmである。
辺ACの中点をM,辺ADの中点をNとし、辺BC,辺ED上
にそれぞれPC=QD=3cmとなる点P,Qをとる。
面MPQNで正四角錐を2つに切断したときに
できる小さいほうの立体の体積を求めよ。
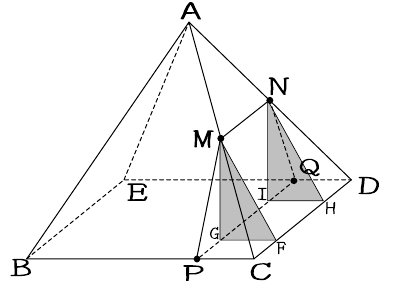
このままの形では体積は出せないので
立体を分けて体積を出す。Mを通り
面BCDEに垂直な面でこの立体を切断する。
Mから面BCDEに垂線をおろし
その交点をGとする。GF//BCとなるよう
にCD上にFをとる。この面MGFが
切断面である。同じように面NIHでも切断
すると四角錐MPCFGと三角柱MGFNIHと
四角錐NIHDQの3つの立体に分かれる
→図1
図１
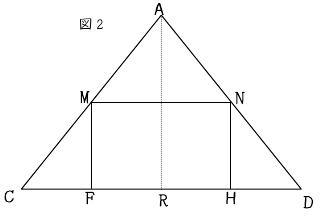
△ACDを平面図にしたものが図2である。
AからCDに垂線を引いて交点をRとしている。
MがACの中点なのでFはCRの中点となり
CF=3cmとなる。
図２
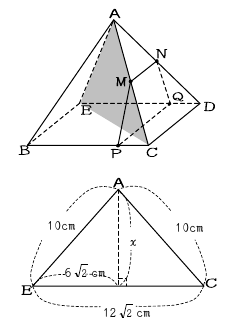
四角錐ABCDEの高さを出す。
図3のように△AECを考えると、
EC=122 ,AE=AC=10の二等辺三角形である。
するとAから垂線をおろせばECの中点
に交わる。垂線の長さをxとして
三平方の定理に当てはめると
x2+(62)2=102
これを解くとx=27となる。
図３
四角錐MPCFGの高さは四角錐ABCDEの半分なので 7cmである。
底面は一辺3cmの正方形なので四角錐MPCFGの体積は
3×3×7÷3=37となる。 四角錐NIHDQも同じ。
次に三角柱MGFNIHの体積
MG= 7, GF=3, FH=6なので
体積は 7×3÷2×6=97 となる。
よって求める立体の体積は 37 +37 +97=157
3
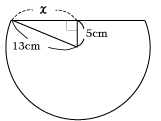
図は半径13cm の球を平面で切ったものである。中心から切り口の
平面までの距離が5cm である。切り口の円の面積を求めよ。
まず、この立体の断面図を描く。・・・図1
球の半径が13cm, 中心から切り口の平面までの
距離が5cmを利用して図のような直角三角形ができる。
切り口の半径をxとして
三平方の定理に当てはめる。
すると x2+52=132
よってx=12 となる。
図１
つまり切り口は半径12cmの円となる。
よって面積は144πcm2 である。
4
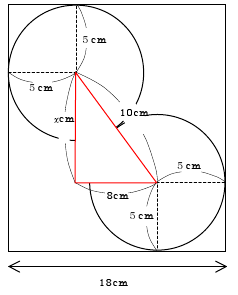
底面の円の半径が9cmの円柱形の容器に
半径5cmの球を2個入れ、球がちょうど
つかるまで水を注いだ。
底面から水面までの高さを求めよ。
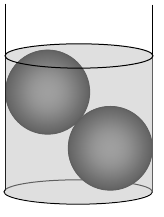
立体を真横から見た図を平面図を描く。・・・図1
図１
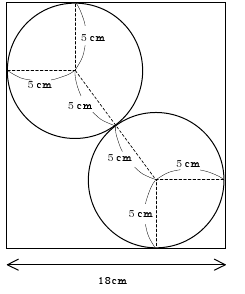図2のように直角三角形(赤)をつくることができる。
斜辺が10cm, 残りの辺が8cmとxcmとして
三平方の定理にあてはめる。
100 = x2+64
x2=36
x=±6
0<xなので
x=6
よって水面までの高さは6+5+5=16となる。
図２
