1. 図で放物線mはy=x2で、nはy=ax+bである。
交点Aのx座標は-1, 交点Bのx座標は3である。
(1) 頂点Oを通り△AOBの面積を2等分する直線の式を求めよ。
(2) 直線nの切片をCとすると△AOCと△BOCの面積比を求めよ。
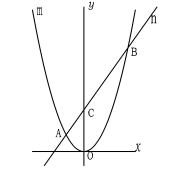
(1) まずAとBの座標を求める。
Aはx = -1なので放物線mの式y=x2 に代入して
y = 1となり A(-1, 1)
同じようにしてBはx = 3をmの式に代入して
y = 9となり B(3, 9)
頂点Oを通り、△AOBの面積をニ等分する直線は、
線分ABの中点を通る。
A(-1, 1)とB(3, 9)の中点は(1, 5)となる。
(0, 0)と(1,5)を通る式は y = 5x である。
(2) 高さが同じ三角形では底辺の長さの比は面積比と等しくなる。
△AOCと△BOCはAC, BCを底辺としたときに頂点Oが共通なので
高さが同じになる。そのため底辺の比AC : BCが面積比と等しく
なる。
(1)で出した座標を使うとAC : BC = 1 : 3なので面積比は1:3である。
2. 図で放物線mはy=3x2, nはy=x2である。
点A, Bは放物線m上の点、点C,Dはn上の点で、
辺ABとCDはx軸に平行で、ADとBCはy軸に平行である。
四角形ABCDが正方形になるときのAの座標を求めなさい。
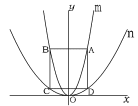
点Aのx座標をpとする。AとDはx座標が同じなので点Dのx座標もpである。
点Aは放物線m上の点なのでy座標は3p2となる。
点Dは放物線n上の点なのでy座標はp2となる。
点Bは点Aとy座標が同じなのでx座標は-pである。
A(p, 3p2), B(-p,3p2), D(p, p2)
四角形ABCDが正方形になるので辺ABの長さと辺ADの長さが等しくなる。
ABの長さはAのx座標からBのx座標を引いて p-(-p)=2p,
ADの長さはAのy座標からDのy座標を引いて3p2-p2=2p2
これらが等しいので 2p2=2p
この2次方程式を解くとx=1となる。よってAの座標(1,3)
放物線と図形 3 放物線と図形の4 放物線と図形の5
