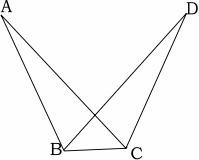
1 右の図で、ＡＢ＝ＤＣ、ＡＣ＝ＤＢならば
△ＢＡＣ≡△ＣＤＢであることを証明せよ。
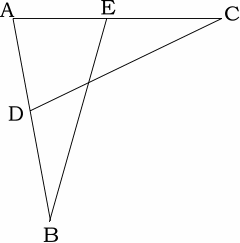
2 AD=AE, ∠ADC=∠AEBのとき
△ACD≡△ABEとなることを証明せよ。
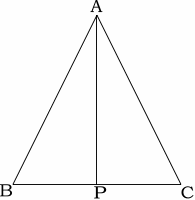
3 図でAB=AC、Pは辺BCの中点である。
このとき△ABP≡△ACPを証明せよ。
4 右の図で、ＯＣは∠ＡＯＢの二等分線である。
ＯＤ＝ＯＥとするとき、△DOP≡△EOPであることを証明せよ。
解説ページに解説がない問題で、解説をご希望の場合はリクエストを送信してください。 解説リクエスト
平行と合同 例題
対頂角錯角・同位角平行線になる条件平行線の錯角・同位角 補助線を引く問題 三角形の内角と外角の関係 印をつけた角の和 多角形の内角・外角いろいろな多角形平行線と多角形折り返した図形角の二等分線と内角の和角の二等分線と内角外角角の二等分線と外角の和角の二等分線(入試レベル)角の二等分線三等分線(入試レベル)三角形の合同証明1 三角形の合同証明2(辺の共通) 三角形の合同証明3(角の共通)三角形の合同証明4(角の二等分線)三角形の合同証明5(平行線の利用)三角形の合同証明6(平行線の利用2)平行線になる証明垂直になることを証明内角の和を利用した証明垂直二等分線を使った証明折り返した図形の証明
△BACと△CDBにおいて
AB=DC (仮定)
AC=DB (仮定)
BC=CB (共通) よって３組の辺がそれぞれ等しいので
△BAC≡△CDB
△ACDと△ABEにおいて
AD=AE (仮定)
∠ADC=∠AEB(仮定)
∠DAC=∠EAB(共通)
よって１組の辺とその両端の角がそれぞれ等しいので
△ACD≡△ABE
△ABPと△ACPにおいて
AB=AC(仮定)
BP=CP (PはBCの中点)
AP＝AP(共通)
よって３組の辺がそれぞれ等しいので
△ABP≡△ACP
△DOPと△EOPにおいて
∠DOP=∠EOP (OCが∠AOBの二等分線)
OD=OE (仮定)
OP=OP (共通)
よって２組の辺とその間の角がそれぞれ等しいので
△DOP≡△EOP
学習 コンテンツ
学習アプリ
中1 計算問題アプリ 正負の数
中1数学の正負の数の計算問題 加法減法乗法除法、累乗、四則計算