2乗に比例する関数 変域、変化の割合

変域

変域とは・・・グラフの範囲のこと。
グラフを描いたときの横の範囲がxの変域、縦の範囲がyの変域になる。

図1 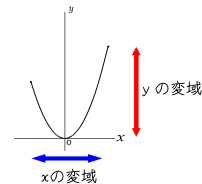図2

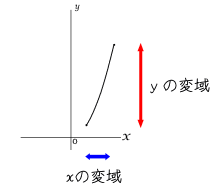
上記図2のような場合や、1次関数ではグラフの両端の点を考えるだけだったが、 図1のように放物線のグラフが原点を含むような場合はyの最小値が0になるので注意が必要になる。 変域を考える場合にはグラフを描くか、少なくとも頭の中に思い浮かべることが大切。 基本的な問題よりもむしろ応用発展問題を解く場合に差がついてくる。

【確認】y = 3x²　について、xの変域が次のそれぞれの場合のyの変域を求めよ。
(1)-5≦x≦-1 (2)-2≦x≦3 (3)1≦x≦4

【答】(1)3≦y≦75　　(2)0≦y≦27　　(3)3≦y≦48

変化の割合

変化の割合= yの増加量 xの増加量

比例反比例、1次関数、そして2乗に比例する関数、変化の割合はすべて同じ式を用いる。
ただし、1次関数では変化の割合は一定だが、2乗に比例する関数では変化の割合は一定にならない。

y=3x²　についてそれぞれの場合の変化の割合をもとめる。
xが−3から1まで変化するとき xが1から5まで変化するとき ①　xが-3から1まで変化するときの変化の割合
x=-3のとき y = 27, x=1のとき y = 3
xが-3から1まで変化する …xの増加量4
yが27から3まで変化する …yの増加量-24
変化の割合は　 −24 4 =−6 ②　xが1から5まで変化するときの変化の割合
x=1 のとき y = 3, x=5のとき y = 75
xが1から5まで変化する …xの増加量4
yが3から75まで変化する …yの増加量72
変化の割合は　 72 4 =18

【確認】
(1)　y=2x²　についてxの値が次のように変化するときの変化の割合をそれぞれ求めよ。
①-3から1 ② -2から4
(2)　 y= 1 4 x² についてxの値が次のように変化するときの変化の割合をそれぞれ求めよ。
① -10から2 ②　-2から6

【答】(1)① -4　② 4　(2)① -2 ②1