2次方程式の文章題

2次方程式文章題を解く手順

1.　何をxで表すか決める
2.　問題文中の数量をxで表し、数量の関係を見つけて方程式にする。
3.　2次方程式を解く。
4.　解が問題に適しているか確かめる。

2次方程式では条件によって答が2通りになることも、1通りのこともある。

数に関する2次方程式文章題

自然数や、正の数という条件があればx>0となる。
【例題】
大小 2 つの数がある。 その差は 8 で積が 48 である。このような２数を全て求めよ。 連続する3つの自然数がある。小さいほうの2数の積の3倍は、大きいほうの2数の積の2倍より50大きい。
この3つの自然数を求めよ。
解説動画① ≫
① 大きいほうの数をxとする。差が8なので、小さい方の数は(x-8)である。
2数の積が48なので　x(x-8)=48
この方程式を解くと
x² -8x -48=0
(x-12)(x+4)=0
x = 12, -4
x = 12のとき 小さい方の数は 12-8=4
x - -4のとき、小さい方の数は -4 -8=-12
答 12と4, -4と-12

② 一番小さい数をxとすると、連続する3つの自然数はx, (x+1), (x+2)となる。
小さい方2数の積の3倍は 3x(x+1)
大きい方2数の積の2倍は 2(x+1)(x+2)
3x(x+1)が2(x+1)(x+2)より50大きいので
3x(x+1) = 2(x+1)(x+2)+50
この方程式を解くと
3x²+3x = 2x²+6x+54
x² -3x -54=0
(x-9)(x+6)=0
x = 9, -6 ところがxは自然数なのでx>0より x=9
答 9, 10, 11

【確認】答表示
大小2つの数がある。その差が4で積が96である。この2数を求めよ。
大きい方の数をxとする。
x(x-4)=96　【答】12と8, -8と-12 大小2つの数がある。その和が6で積が-16である。この2数を求めよ。
大きい方の数をxとする。
x(6-x)=-16　【答】8と-2 連続する3つの自然数がある。小さいほう2数の積の3倍は大きい方2数の積の2倍より6小さい。この3つの自然数を求めよ。
一番小さい数をxとする。
3x(x+1)=2(x+1)(x+2)-6　【答】2と3と4、1と2と3 連続する3つの自然数がある。それぞれの数を2乗した数の和が50になる。この3つの自然数を求めよ。
最も小さい数をxとする。
x²+(x+1)²+(x+2)²=50
これを解くとx=3, -5
xは自然数なのでx>0よりx=3
【答】3, 4, 5

平面図形に関する問題

長さや面積に負の数はないので、その場合x>0となる。
【例題】 ある正方形がある。この正方形の縦を10cm伸ばし、横を2㎝縮めてできた長方形の面積は、もとの正方形の面積の2倍より20㎝²小さくなった。　もとの正方形の1辺の長さを求めよ。 周の長さが38cm, 面積 84cm²の長方形の縦と横の長さを求めよ。ただし、横のほうが長いとする。
①解説動画 ≫ ②解説動画 ≫ ① もとの正方形の1辺の長さをxcmとすると、長方形の縦は(x+10)cm, 横は(x-2)cmである。
もとの正方形の面積がx²cm², 長方形の面積が (x+10)(x-2)cm²
長方形の面積はもとの正方形の面積の2倍より20小さいので
(x+10)(x-2) = 2x²-20
これを解くと
x²+8x-20 =2x²-20
-x²+8x=0
x(x-8)=0
x = 0, 8　ところがx>0よりx=8
【答】 8cm

② 周の長さが38cmなので、縦と横の長さの合計が19cmである。
縦の長さをxcmとすると横の長さは(19-x)cm
面積が84cm²なので
x(19-x)=84
これを解くと
19x-x²=84
x²-19x+84=0
(x-7)(x-12)=0
x=7, 12
横のほうが長いのでx=7
【答】 縦7cm, 横12cm

【確認】答表示
正方形の縦を9cm伸ばし、横を1㎝縮めてできた長方形の面積は、もとの正方形の面積の2倍より42㎝²小さくなった。　もとの正方形の1辺の長さを求めよ。
もとの正方形の1辺をxcmとする
(x+9)(x-1)=2x²-42
これを解くとx=11,-3
x>0よりx=11【答】11cm 周の長さが44cm, 面積 117cm²の長方形の縦と横の長さを求めよ。ただし、横のほうが長いとする。
縦の長さをxcmとする。
x(22-x)=117
これを解くとx=13, 9
横の長さのほうが長いので x=9【答】縦9cm, 横13cm 横が縦より8cm長い長方形がある。この長方形の面積が84cm²のとき、縦と横の長さを求めよ。
縦の長さをxcmとする。
x(x+8)=84
これを解くとx =6, -14
x>0よりx=6 【答】縦6cm, 横14cm

動点に関する2次方程式文章題

毎秒1cmで進む点がx秒間に進む道のりはxcm, 毎秒2cmなら2xcmとなる。
【例題】　 △ABCはBC=12㎝、AC=6㎝、∠BCA=90°の直角三角形である。
点Pは頂点Bを出発して毎秒2㎝でCまで進む。
同時に点Qは頂点Cを出発して毎秒1㎝でAまで進む。
△PCQの面積が9㎝²になるのは出発から何秒後か。 解説動画 ≫
△PCQの面積をxの式で表し、「△PCQの面積が9になる」という方程式を作る。
三角形の面積は底辺×高さ÷2、△PCQは直角三角形なので、辺PCと辺QCをそれぞれxの式で表す。

Pは毎秒2cmで進むのでx秒間に進む道のりは2xcmである。
出発からPが進んだ長さはBPなのでBP=2xとなるのでPC=12-2xである。
Qは毎秒1cmなのでx秒間に進む道のりはxcmになる。
出発からQが進んだ長さはCQなのでCQ=x
△PCQの面積をxの式で表すとx×(12-2x)÷2 = x(6x-x)
これが9cm²なので　x(6-x)=9
これを解くと6x-x²=9
x²-6x+9=0
(x-3)²=0
x=3
　　　　　　　 【答】3 秒後

【確認】答表示
1辺18㎝の正方形ABCDにおいて点Pは頂点Aから頂点Bまで、
点Qは頂点Dから頂点Aまで動く。PとQは同時に出発し
両方とも毎秒1㎝の速さで動くとする。
△QPCの面積が126㎝²になるのは出発してから何秒後か。
出発から x 秒後とする。
　　 18(18−x) 2 + x(18−x) 2 + 18x 2 =324-126
　　 これを解くと x=6, x=12
　　　　　　　 【答】6 秒後と 12 秒後 図は縦12㎝、横6㎝の長方形である。
点Pは頂点Aを出発して毎秒2㎝でBまで動き、点QはAと同時に
頂点Dを出発し毎秒1㎝でAまで動く。Pから辺BCに平行な直線
を引き辺CDとの交点をRとする。
台形PRDQの面積が16cm²になるのは出発してから何秒後か。
出発から x 秒後とする。
6×2x 2 + x×2x 2 =16
　　 これを解くと x=2, x=-8
　　 ところが 0<x なので x=2
　　　　　　　 【答】2 秒後

座標平面での図形に関する文章題

グラフ上の点は、グラフの式に代入して求める。
例えば、y=2x+3のグラフ上の点の座標はx座標をpとすると(p, 2p+3)である。
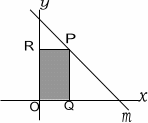
【例題】　 図で直線mはy=-x+12 のグラフである。
Pは直線m上の点でPからx軸にひいた垂線をPQ,
y軸に引いた垂線をPRとする。
四角形PROQの面積が20になるときのPの座標を求めなさい。
解説動画 ≫ Pはy=-x+12のグラフ上の点なので
x座標をpとするとy座標は-p+12
よってPRの長さがp, PQの長さが-p+12となる。
長方形の面積 = 縦×横なので
20 = p(-p+12)
20 = -p²+12p
p² -12p +20=0
(p-2)(p-10)=0
p=2, 10
よってP(2, 10) または(10,2)

【確認】答表示
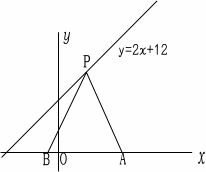
図で点P は直線y=2x+12上のx>0の部分にある点で、
点Aは(10,0)である。AP=BPとなるように点Bをx軸上にとり、
二等辺三角形PBAを作る。
△PBAの面積が120になるときのPの座標を求めなさい。 Pのx座標をxとする。
　　 2×12(2x+12)(10-x)=120 　　これを解くとx=4,　x=0
　 　　ところがx>0なので　x=4
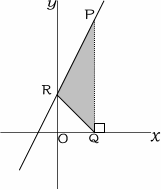
　　【答】　(4, 20) 点Pはy=2x+4のグラフ上の点でx>0である。
Pからx軸におろした垂線の交点をQとする。
Rは切片である。△PQRの面積が15になるときのPの座標を求めなさい。 Pのx座標をxとする。
x(2x+4) 2 =15 これを解くとx=3,　x=-5
　ところがx>0　なので　x=3
　　【答】　(3, 10)

割合に関する文章題

割合のもとになる数に注意する。
例えば、原価の3割の利益を見込んだ値段は 原価×1310で、
定価の3割引の値段は 定価×710 である。
【例題】　 原価400円の品物に2x割の利益を見込んで定価をつけた。売り出しの日に定価のx割引で売った。利益が48円だった。xの値を求めよ。
解説動画 ≫ 原価400円の2x割の利益を見込んだ定価は400×10+2x10(円)
この定価に対してx割引きするので安売りの値段は 400×10+2x10×10-x10
原価400円で、利益が48円なので、448円で売ったことになる。
よって式は400×10+2x10×10-x10=448
4(10+2x)(10-x)=448
(10+2x)(10-x)=112
100+10x-2x²=112
2x²-10x+12=0
x²-5x+6=0
(x-2)(x-3)=0
x=2,3　

【確認】答表示
原価400円の品物に2x%の利益を見込んで定価をつけた。売り出しの日に定価のx%割引で売った。利益が50円だった。xの値を求めよ。
400×100+2x100×100-x100=450

【答】x=25 原価800円の品物にx%の利益を見込んで定価をつけた。売り出しの日に定価のx%割引して売ったら18円損してしまった。 xの値を求めよ。ただしx>0とする。
800×100+x100×100-x100=782
これを解くとx=15, -15ところがx>0より x =15
【答】x=15