座標平面での図形に関する文章題
グラフ上の点は、グラフの式に代入して求める。
例えば、y=2x+3のグラフ上の点の座標はx座標をpとすると(p, 2p+3)である。
【例題】
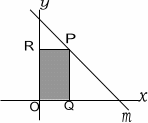
図で直線mはy=-x+12 のグラフである。
Pは直線m上の点でPからx軸にひいた垂線をPQ,
y軸に引いた垂線をPRとする。
四角形PROQの面積が20になるときのPの座標を求めなさい。
解説動画 ≫
Pはy=-x+12のグラフ上の点なので
x座標をpとするとy座標は-p+12
よってPRの長さがp, PQの長さが-p+12となる。
長方形の面積 = 縦×横なので
20 = p(-p+12)
20 = -p2+12p
p2 -12p +20=0
(p-2)(p-10)=0
p=2, 10
よってP(2, 10) または(10,2)
【確認】
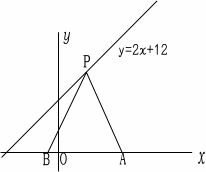
図で点P は直線y=2x+12上のx>0の部分にある点で、
点Aは(10,0)である。AP=BPとなるように点Bをx軸上にとり、
二等辺三角形PBAを作る。
△PBAの面積が120になるときのPの座標を求めなさい。
Pのx座標をxとする。
2×12(2x+12)(10-x)=120
これを解くとx=4, x=0
ところがx>0なので x=4
【答】 (4, 20)
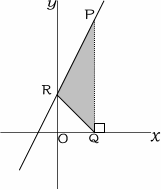
点Pはy=2x+4のグラフ上の点でx>0である。
Pからx軸におろした垂線の交点をQとする。
Rは切片である。△PQRの面積が15になるときのPの座標を求めなさい。
Pのx座標をxとする。
x(2x+4)
2
=15
これを解くとx=3, x=-5
ところがx>0 なので x=3
【答】 (3, 10)
