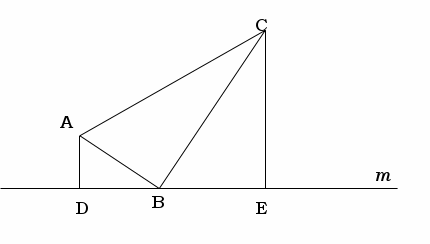
1. ∠ABC=90°の直角三角形の頂点A, Cから直線mにそれぞれ垂線を
おろし、交点をD, Eとする。このとき△ADB∽△BECを証明しなさい。
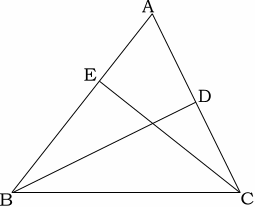
2. △ABCの頂点B, Cからそれぞれ辺AC, ABに垂線を引き、交点をそれぞれD, Eとする。
(1) △ABD∽△ACEを証明せよ。
(2) AB=9cm, AC=8cm, DがACの中点のときAEの長さを求めよ。
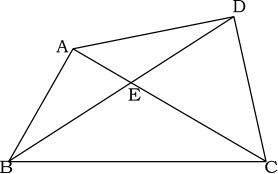
3. 四角形ABCDにおいて対角線AC, BDの交点をEとする。
∠ABE=∠EBC, CD=CEが成り立っているとき、
△ABE∽△CBDとなることを証明せよ。
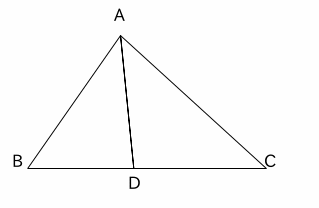
4. 右の図でAB=6㎝, BD=4㎝, DC=5㎝, AD=4.5㎝である。
(1) 相似な三角形の組を一組答えよ。
(2) (1)を証明しなさい。
(3) ACの長さを求めなさい。
相似 例題
相似 基本問題1 相似 基本問題2 二等辺三角形を使った相似の証明 平行四辺形と相似の証明 正三角形と相似の証明 直角三角形と相似の証明 折返した図形の相似の証明 二等辺三角形と相似の証明 垂直を使った相似の証明 三角形と線分 台形と線分 平行四辺形と線分比 平行四辺形と線分比2 相似比と線分1 相似比と線分2 相似と線分比1(平行四辺形) 相似と線分比2 平行線と線分の長さ 中点連結定理1 中点連結定理2 角の二等分線と辺の比1 角の二等分線と辺の比2 円と相似1円と相似2線分の比と面積比 基礎問題相似な図形の面積比相似な図形の面積比、体積比線分の比と面積比線分の比と面積比2 相似比と線分の長さ(入試レベル) 相似と面積比(入試レベル) 相似と線分の長さ(入試レベル)相似と線分比・面積比(入試レベル) 相似な図形の面積比、体積比(入試レベル)立体表面の最短経路(入試レベル)
△ADBと△BECにおいて
三角形の内角の和は180°なので∠ADB+∠DAB+∠ABD=180°
∠ADB=90°(垂線)より∠DAB+∠ABD=90°・・・①
直線の角は180°なので∠ABD+∠ABC+∠CBE=180°
∠ABC=90°(仮定)より∠ABD+∠CBE=90°・・・②
①、②より∠DAB=∠CBE・・・③
∠ADB=∠BEC=90°(垂線)・・・④
③、④より2組の角がそれぞれ等しいので△ADB∽△BEC
(1)
△ABDと△ACEにおいて
∠BAD＝∠CAE（共通）
∠BDA=∠CEA＝９０°（仮定）
よって2組の角がそれぞれ等しいので△ABD∽△ACE
(2)
32
9
cm
△ABEと△CBDにおいて
∠AEB=∠DEC(対頂角)・・・①
CD=CEより2辺が等しいので△CEDは二等辺三角形
よって∠DEC=∠EDC(二等辺三角形の底角)・・・②
①、②より∠AEB=∠CDB・・・③
∠ABE=∠EBC(仮定)・・・④
③、④より2組の角がそれぞれ等しいので△ABE∽△CBD
(1) △ABCと△DBA
(2)
△ABCと△DBAにおいて
AB:DB=6:4=3:2(仮定)
BC:BA=9:6=3:2(仮定)
よってAB:DB=BC:BA・・・①
∠ABC=∠DBA(共通)・・・②
①、②より2組の辺の比とその間の角がそれぞれ等しいので△ABC∽△DBA
(3)
27
4
cm
学習 コンテンツ
学習アプリ
中1 方程式 文章題アプリ
中1数学の方程式文章題を例題と練習問題で徹底的に練習