式の計算の利用

x²+2x+a を因数分解すると、(x+3)(x+m) になるという。mとaの値を求めなさい

　次のことがらを証明しなさい。

(1)図のように1辺の長さがa,bの大小2つの正方形が並べてある。この2つの正方形の面積の差はc,dの積に等しい。

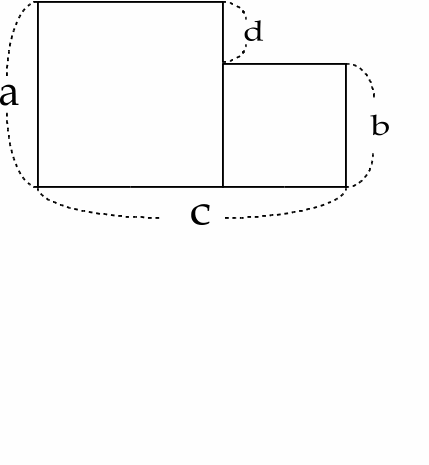
(2)２つの連続した奇数の積に１をたすと４の倍数になる。

(3)２つの連続する奇数の平方の差は８の倍数になる。

(4)３つの連続した偶数では最も大きい数の平方から残りの２つの数の積をひいた差は４の倍数になる。

1.
m=-1,　 a=-3

2.
(1)　この 2 つの正方形の面積の差は
　　a²-b²…①
　　c=a+b,　 d=a-b なので
　　c と d の積は
c×d = (a+b)(a−b) = a²−b² …②
　　①、②よりa²-b²=c×d
　　よってこの 2 つの正方形の面積の差は c, d の積に等しい

(2) mを整数として２つの連続した奇数を 2m-1,　2m+1 とする。
　　それらの積に 1 をたすと、
(2m-1)(2m+1)+1 = 4m²−1+1 = 4m²
　　m は整数なので m²も整数。
　　よって4m²は4の倍数となる。

(3) mを整数として２つの連続した奇数を2m-1,　2m+1とする。
　　平方の差は
　　(2m+1)²-(2m-1)²=4m²+4m+1-(4m²-4m+1)=8m
　　m は整数なので 8m は 8 の倍数となる。

(4) mを整数として、3つの連続した偶数を2m,　2m+2,　2m+4とする。
　　もっとも大きい数の平方から残りの2数の積を引くと
(2m+4)²−2m(2m+2)= 4m²+16m+16−4m²−4m =12m+16 =4(3m+4)
　　mは整数なので3m+4 も整数となり4(3m+4) は4の倍数となる。